[go back to Tacelli’s previous argument]
The nature of infinity
Greg Raven
Let me start by stating that I am comfortable with the thought that I may never know how, where, or why the universe came into being. I don’t think that the origin of the universe is knowable or, as in the case of the big bang
theory, that the moment before the origin of the universe is knowable, which to my mind amounts to the same thing.
From what I can tell of the Kalam Argument, it depends to a great extent on several misconceptions about infinity. I will try to address them all.
Infinity is not a number
Infinity is not a number, but rather a representation of some unspecified, arbitrarily large number. Therefore, to talk of counting to infinity, or counting backwards from infinity (!) is nonsensical.
There is more than one ‘infinity’
The Kalan Argument tries to force the discussion into a corner by eliminating all but something called actual infinity.
That is, it attempts to reject theoretical infinities such as the familiar line we all met in geometry that extends to infinity in both directions. Because the line, as defined in geometry, is an imaginary construct, it may safely be disregarded for discussions about the nature of God and the origin of the universe.
The Kalam Argument also seeks to invalidate the infinity of starting at zero (for example) and counting upward toward infinity. This is referred to as a potential infinity, because — count as you will — you will never reach
infinity (a restatement of the erroneous implication that infinity is an actual number that could be reached). This is a flawed argument, as I shall demonstrate below, although even if it is granted that this type of infinity can never be more than a potential infinity, this still does not save the Kalam Argument, as also shall be shown.
A third type of infinity is one not mentioned in versions of the Kalam Argument I have seen, and that is of what might be called a circular infinity. A circle has no beginning or end, and one could travel in a circle for any length of time and never run out of circle along which to travel. I should mention that other shapes (such as a square) could be said to be infinity in this same way, although I don’t wish to disturb anyone with a concept of infinity with punctuation marks.
If a circle seems too simple to be the basis for any rigorous philosophising, I give you the continuum between pure information and pure entropy. A system of maximum information would also have maximum order, by definition. A system of maximum entropy would have maximum disorder. Paradoxically, however, in a maximally ordered system, each new piece of data contributes a minimal amount of new information, and in a maximally disordered system, each new piece of data contributes a maximal amount of new information. Be that as it may, with or without the circle infinity, there is still no hope for the Kalam Argument.
There is a fourth type of infinity that I believe destroys the Kalam Argument, as it is by definition an actual infinity. The existence of this actual infinity highlights one of the core problems with the Kalam Argument.
The first step to an 'actual' infinity
Because understanding the nature of this actual infinity may be difficult, I am going to sneak up on it, using as an illustration an example of a simple, potential infinity, before making the jump to an actual infinity.

Imagine an equilateral triangle, that is, one with three equal sides and three equal corner angles. One of the natures of the triangle is that for any given triangle, there is a circle that can be said to intersect the apexes of the triangle. For this triangle, if we give each side a length
of one unit, then the sum of the sides — that is, the length of the boundary — is 3 units. The circumference of the enclosing circle could be calculated, but all that is important for this discussion is the acknowledgement that it is finite, as is the area enclosed by the circle.
So far, we have a circle, with a triangle within, its three apexes intersecting the circumference of the circle in such a way that the portions of the circle between intersections are three arcs of equal length.
Now, beginning with the triangle, at the middle of each side, add a new triangle one-third the size, with its base laying along the existing side. You now have a six-pointed star, commonly known as a Star of David.

Because you have added three smaller triangles to the outside of the original triangle, you have increased the length of the boundary. Where originally you had:
1 + 1 + 1 = 3
you now have:
1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3 = 12/3 = 4
The sections are smaller, but there are more of them. This increase can be expressed:
3 × 4/3
If you repeat this operation of adding triangles in the middle of each new side, one-third the size of the side, you wind up with a spikey-looking Star of David, which has a boundary length of:
3 × 4/3 × 4/3

Do it once more, and the Star of David begins to look fuzzy, although still generally six-pointed. The boundary length would then be:
3 × 4/3 × 4/3 × 4/3

However, you can continue adding smaller and smaller triangles endlessly, at which time the formula for the length of the boundary would be:
3 × 4/3 × 4/3 × 4/3 … — infinity
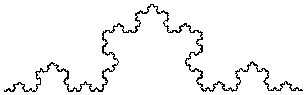
No matter how many times you add new triangles to the middle of the segments of your polygon (which goes by the name the Koch Snowflake), you can always add more. Because each new round of added triangles is one-third the size of the existing sides, they never intersect each other — there is always plenty of room to add new triangles.
However, while the length of the boundary of your snowflake increases toward infinity, the area does not, as can be seen be the fact that at no time do any of the points fall outside of the surrounding circle, and we know that the circle has both a finite circumference and area. Therefore, a line of [potentially] infinite length is contained in a finite area.
The normal protest must naturally be that one could never have enough time to add an infinite number of smaller triangles, so this Snowflake is only a potential infinity. There is a major flaw in this argument, but I will grant the potential
nature of this infinity. My purposes in proposing this construct have been fulfilled: 1) it is a simple enough construct that nearly everyone should be able to grasp it, and 2) there is a mathematical representation of this construct. This type of construct is one form of an object known as a fractal,
which the OED2 defines as, a mathematically conceived curve such that any small part of it, enlarged, has the same statistical character as the original.
An ‘actual’ infinity
One of the impediments to this construct being considered an actual
infinity is that it requires steps toward infinity to demonstrate the concept of infinity. Not only must you add smaller and smaller triangles to greater and greater numbers of sides, but to calculate the length of the boundary, you must multiply the length of the boundary from the previous, unaltered polygon by 4/3 to get the new boundary length after the addition of the triangles.
But what if there was a mathematic expression that did not require this step-by-step approach? An expression that contained everything in itself to create an actual
infinity? As it turns out, there are several such mathematical expressions, the most famous of which surely is that which, when calculated and plotted, generates what is called a Mandelbrot curve. The Mandelbrot curve appears as a cardiod with smaller circular attachments, each with its own smaller circular attachments. An example of the Mandelbrot curve is shown here.

Because of the nature of the mathematical expression that defines a Mandelbrot curve, each part of the curve statistically resembles any other part of the curve. The characteristic holds true no matter how closely you examine the curve. You could, for example, zoom in
on a minute segment of the curve shown above, and your examination would reveal a galaxy of new curves, with numberless new cardiod shapes lurking everywhere. Each of those cardiod shapes, similar but not identical to the original shape, can in turn be examined at any zoom factor
with the same results as the original examination. I maintain that this curve represents an actual infinity.
This now brings us to the main failing of the Kalam Argument. Assume for a moment that the Mandelbrot curve represents an actual infinity. How would a human being verify such a claim? If infinity
were a number, one could substitute infinity
for one of the terms of the Mandelbrot equation, and thus zoom
to the maximum level, but this is fallacious thinking. No matter what numerals one substitutes for the variables in the Mandelbrot equation, there are always higher (and lower) numerals that could be substituted in: you can never reach the end of it. This is not a limitation of the Mandelbrot equation or even the number system, but rather of our human ability to perceive infinity.
Postscript: God as the cause
An argument that has been made is that because the universe came into being, there was a cause for it coming into being, and this cause could only have been the Creator, God.
God may exist, and may have created the universe, but there is an alternative, which is that the universe came into being because the potential was there for it to come into being. This potential could have manifested itself in other ways, but in this case, it manifested itself in the formation of the universe.
read Tacelli’s response
